Чертеж куба формула расчета геометрических величин

 Чертеж куба формула расчета геометрических величин, которые можно применить к прямоугольному параллелепипеду, то есть, когда все ребра одинаковой длины.

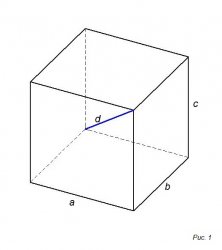
Посмотрим на рисунок 1, где обозначены геометрические величины куба:

• a, b, c – ребра: a = b = c
  
• d – диагональ
  

Зная из размеры, можно по формулам рассчитать диагональ(d), площадь (S) и объем (V)

d² = 3a²

S = 6a²

V = a³

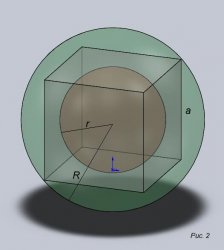
Посмотрим на рисунок 2, где:

• r – радиус вписанной окружности
  
• R – радиус описанной окружности
  

По формулам определяем:

r = ½ a;

R = ½ a√3

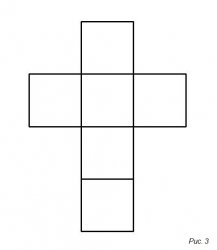
На рисунке 3 изображена развертка куба

Свойства геометрической фигуры:

• если провести четыре сечения через центр под углом девяносто градусов к главным диагоналям, получим правильный многоугольник;
  
• в объем куба вписываются правильные многогранники:
  - тетраэдр, двумя способами, который составит одну треть от объема;
  - октаэдр, двумя способами;
  - икосаэдр.
  

На рисунке 4, как пример построения,

изображена геометрическая форма модели, которая получилась путем несложных построений. Круглые простые цилиндры одинакового диаметра и одинаковой длины, размещаем перпендикулярно относительно плоскостей, которые пересекают вершину и противоположное нижнее ребро. Экспериментируя с различными геометрическими формами и построениями плоскостей по разным точкам, ребрам и граням, можно получить интересные и замысловатые фигуры. Глядя на них, будет тяжело определить принцип их построений.