Чертеж, призма четырехугольная правильная диагональ, площадь, объем и свойства

 Чертеж, призма четырехугольная правильная диагональ, площадь, объем и свойства, все перечисленные выше показатели разберем подробно

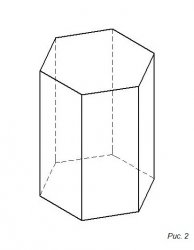
Призма - это фигура изображенная на 1-ом рисунке, у которой равные многоугольники у основания и вершины, а боковыми гранями являются параллелограммы.

Боковую поверхность (М) определяем по формуле: M = pl, где:

• p – периметр сечения (плоскость к ребру под девяносто градусов)
  
• l – ребро
  

Полную поверхность (S) определяем по формуле: S = M +2F, где:

• F – площадь основания
  

Объем (V) определяем по формуле: V = Fh, где:

• h – высота
  

Прямой, называется фигура, у которой ребра находятся под углом девяносто градусов к плоскости основания.
Правильная – если она прямая, и основанием являются правильные многоугольники (все стороны и все углы равны).

Смотрим 2-ой рисунок.

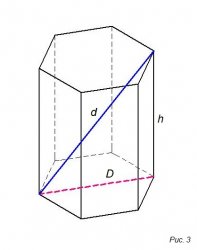
На 3-ем рисунке показана диагональ d

Диагональ (d) определяем по формуле: d = √(D² + h²), где:

• D – диаметр описанной окружности
  
• h – высота
  

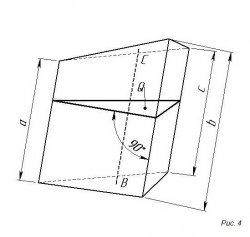
На 4-ом рисунке показана треугольная призма:

Объем (V) определяем по формуле: V = 1/3 (a + b + c)Q, где:

• Q – площадь перпендикулярного сечения
  
• a, b, c – длина ребер
  

Для n-гранной, усеченной не параллельно основанию, объем определяем по формуле: V = lQ, где

• l – длина линии ВС, соединяющая центры тяжести оснований, и перпендикулярна к плоскости Q
  

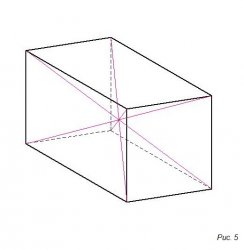
На 5-ом рисунке, у основания параллелограмм, такая фигура называется параллелепипедом.

В параллелепипеде все четыре диагонали пересекаются.

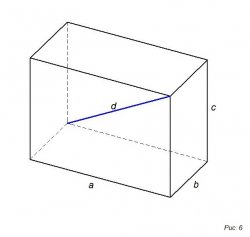
На 6-ом рисунке изображен прямоугольный параллелепипед:

Объем параллелепипеда (V) определяем по формуле: V = abc, где

• a, b, c – длина ребер
  

Диагональ (d) определяем по формуле: d² = a² + b² + c²

Площадь (S) определяем по формуле: S = 2 (ab + bc + ca)

Если выполняется условия равенства ребер a = b = c, то получаем чертеж куба