Формулы параллелограмма чертеж и свойства

 Формулы параллелограмма чертеж и свойства, принятые связи и их взаимодействие между собой.

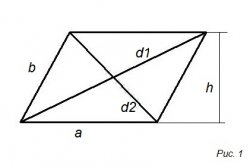
На 1-ом рисунке изображен параллелограмм, основные свойства которого:

• стороны напротив друг друга равны
• стороны напротив друг друга параллельны
• в точке пересечения диагоналей, они делятся пополам
• углы напротив друг друга равны
Наличие у четырехугольника одного из перечисленных свойств, как следствие является и наличием остальных свойств.
Опишем связь между сторонами и диагоналями: d1² + d2² = 2(a² + b²)
S =ah

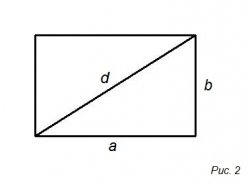
На 2-ом рисунке изображен, в виде прямоугольника, основные свойства которого:

• все углы девяносто градусов (прямые)
• все диагонали равны
S = ab

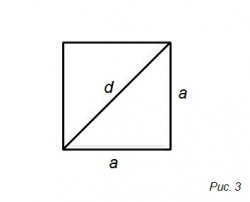
На 3-ем рисунке изображен, в виде квадрата, основные свойства которого:

• все углы девяносто градусов (прямые)
• все стороны равны: a = b
S = a² = ½ d²
d = a√2 ≈ 1,41a
a = ½d√2 ≈ 0,707d

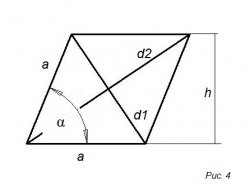
На 4-ом рисунке изображен, в виде квадрата, основные свойства которого:

• все стороны равны

• диагонали расположены под углом девяносто градусов друг к другу
• углы делятся диагоналями пополам
d1 = 2a sin (α/2)
d2 = 2a cos (α/2)
d1² + d2² = 4a²
S = ah = a² sin α = ½ d1d2

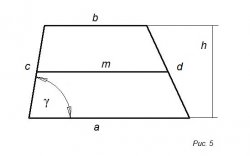
На 5-ом рисунке изображен, в виде трапеции, основные свойства которой:

• две стороны параллельны между собой
• a, b – основания
• h – высота
• m – средняя линия, которая соединяет средины непараллельных сторон, она параллельна основаниям
m = ½ (a + b)
S = ½ (a + b)h = mh
Если d = c, трапеция равнобочная, тогда S = (a – c cos γ) c sin γ = (b + c cos γ) c sin γ

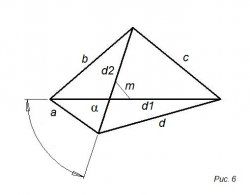
На 6-ом рисунке изображен, в виде четырехугольника, основные свойства которой:

• сумма углов четырехугольника равна триста шестьдесят градусов
• m – отрезок соединяющий центры диагоналей
a² + b² + c² + d² = d1² + d2² +4m²
S = ½ d1d2 sin α

В четырехугольник можно вписать окружность, если a + c = b + d
Четырехугольник можно описать окружностью, если α + γ = β + δ = 180˚
ac +bd = d1d2
S = √((p – a)(p – b)(p – c)(p – d))
p = ½ (a + b + c + d)