Сектор окружности формулы, описание и рисунки
Изучая плоские геометрические фигуры, необходимо четко понимать все определения того или иного обозначения. Правильное их представление позволит быстро и правильно освоить предлагаемые азы теории. И так окунемся в его мир.
• Часть круга, которая ограничена двумя радиусами и дугой окружности, проведенной из одной точки радиуса в другую, будем называть сектором.
• Часть круга, которая ограничена дугой окружности, проведенной из одной точки хорды в другую, будем называть сегментом.
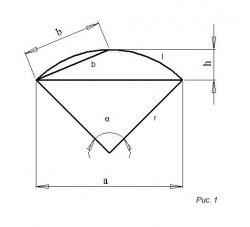
Сектор окружности и его сегмент изображены на 1-ом рисунке, где
r – радиус;
l – длина дуги;
a – хорда;
α – центральный угол (в градусах);
h – стрела сегмента;
S – площадь сектора;
S1 – площадь сегмента
a = 2√(2hr – h²) = 2r sin α/2
h = r – √(r² – a²/4) = r(1 – cos α/2) = a/2 tg α/4
l = 2πrα/360 ≈ 0.01745rα
S = πr²/360
S1 = r²/2 (2πα/180 – sin α) = ½ (lr – a(r – h))
Вспомогательные формулы
l ≈ 0,01745rα ≈ (8b – a)/3 ≈ √(a² + h²16/3)
S ≈ 0,00873r² α
S1 ≈ h/15(6a + 8b)
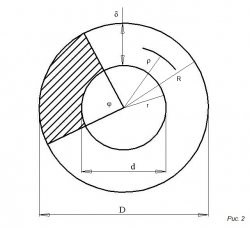
Круговое кольцо изображено на 2-ом рисунке, где
D – внутренний диаметр;
d – внешний диаметр;
R – внешний радиус;
R – внутренний ралиус;
ρ – средний радиус;
δ – толщина кольца;
S – площадь кольца;
S1 – площадь части кольца заштрихованной поверхности
D = 2R
d = 2r
ρ = ½(R + r)
δ = R – r
S = π(R² – r²) = π(D² – d²)/4 = 2πρδ
S1 = φπ(R² – r²)/360 = φπ(D² – d²)/180 = φπρδ/180
Дополнительные формулы окружности применяются при чертеже круга.
Надеемся, что полученная информация пригодится в решении различных задач и вопросов.


Комментариев нет: