Чертеж цилиндра формулы площади поверхности, другие величины

 Чертеж цилиндра формулы площади поверхности, другие величины, подробно рассмотрим в представленной статье

Примем условные обозначения:
• V – объем
• S – площадь полной поверхности
• М – площадь боковой поверхности
• F– площадь основания
• h – высота

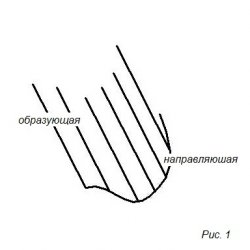
На 1-ом рисунке изображена цилиндрическая поверхность,

Которая образуется прямой линией (образующей), перемещаемой параллельно заданному направлению вдоль кривой (направляющей).

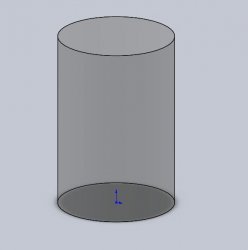
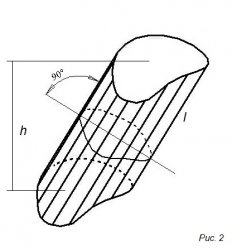
На 2-ом рисунке изображен цилиндр,

Тело ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, являющимися основаниями цилиндра.
Для любого цилиндра:
• р – периметр основания
• s – периметр сечения, перпендикулярного к образующей
• Q – площадь сечения
• l – длина образующей

M = ph = sl
V = Fh = Ql

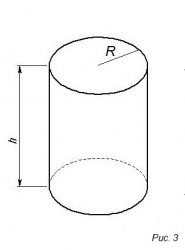
На 3-ем рисунке изображен круглый прямой цилиндр

Имеет в основании чертеж круга, его образующие расположены под углом девяносто градусов к плоскости основания, где:
• R – радиус основания

M = 2πRh
S = 2πR (R + h)
V = πR²h

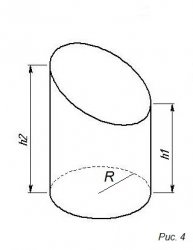
На 4-ом рисунке изображен усеченный круглый,

Имеет в основании круг, его образующие перпендикулярно к плоскости основания.
M = πR (h1 + h2)
S = πR (h1 + h2 + R + √ (R² + ((h2 – h1)/2)²)
V = πR² (h1 + h2)/2

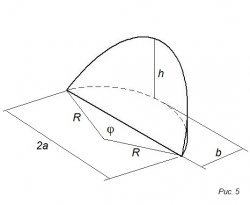
На 5-ом рисунке изображен отрезок

α = ½ φ
V = ⅓ h/b (a (3R² - a²) + 3R² (b – R) α) = hR³/b (sin α - ⅓ sin ³ α – cos α)
M = 2Rh/b ((b – R)α +a))
Формулы действительны, если b ˃ R, φ ˃ π

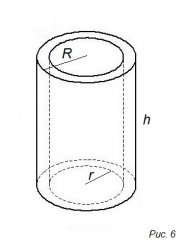
На 6-ом рисунке изображена труба

где:
• R – внешний радиус
• r – внутренний радиус
• ρ – средний радиус

δ = R –r
ρ = ½ (R + r)
V = πh (R² - r²) = πhδ (2R – δ) = πhδ (2r + δ) = 2πhδρ